Secant Method

Secante

View more presentations from oskrjulia.

In numerical analysis, the secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite difference approximation of Newton's method. However, the method was developed independent of Newton's method, and predated the latter by over 3000 years.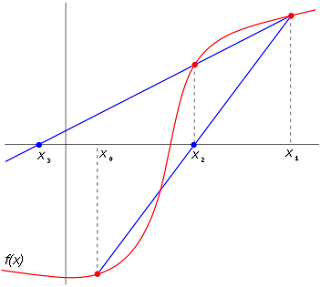 

 The secant method is defined by the recurrence relation

 As can be seen from the recurrence relation, the secant method requires two initial values, x₀ and x₁, which should ideally be chosen to lie close to the root.

Example

#include 
#include 
  
double f(double x)
{
    return cos(x) - x*x*x;
}
  
double SecantMethod(double xn_1, double xn, double e, int m)
{
    int n;
    double d;
    for (n = 1; n <= m; n++)
    {
        d = (xn - xn_1) / (f(xn) - f(xn_1)) * f(xn);
        if (fabs(d) < e)
            return xn;
        xn_1 = xn;
        xn = xn - d;
    }
    return xn;
}
  
int main(void)
{
    printf("%0.15f\n", SecantMethod(0, 1, 5E-11, 100));
    return 0;

  

form f(x) = cos(x) − x³ = 0

After running this code, the final answer is approximately 0.865474033101614. The initial, intermediate, and final approximations are listed below, correct digits are underlined.

The following graph shows the function f in red and the last secant line in bold blue. In the graph, the x-intercept of the secant line seems to be a good approximation of the root of f.